官方链接
https://leetcode-cn.com/problems/shortest-path-in-binary-matrix
在一个 N × N 的方形网格中,每个单元格有两种状态:空(0)或者阻塞(1)。
一条从左上角到右下角、长度为 k 的畅通路径,由满足下述条件的单元格 C_1, C_2, ..., C_k 组成:
相邻单元格 Ci 和 C{i+1} 在八个方向之一上连通(此时,Ci 和 C{i+1} 不同且共享边或角) C_1 位于 (0, 0)(即,值为 grid[0][0]) C_k 位于 (N-1, N-1)(即,值为 grid[N-1][N-1]) 如果 C_i 位于 (r, c),则 grid[r][c] 为空(即,grid[r][c] == 0) 返回这条从左上角到右下角的最短畅通路径的长度。如果不存在这样的路径,返回 -1 。
示例 1:
输入:[[0,1],[1,0]]
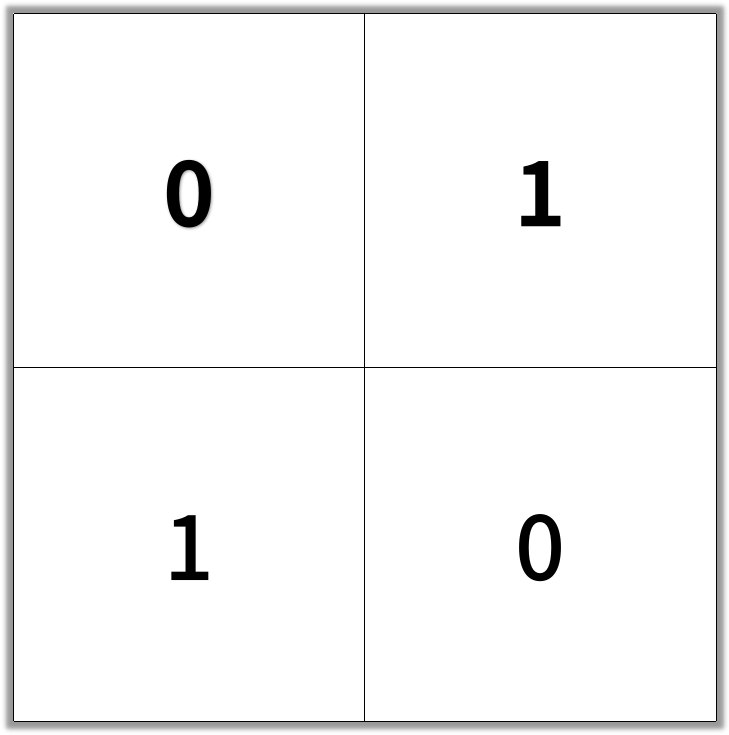 输出:2
输出:2

示例 2:
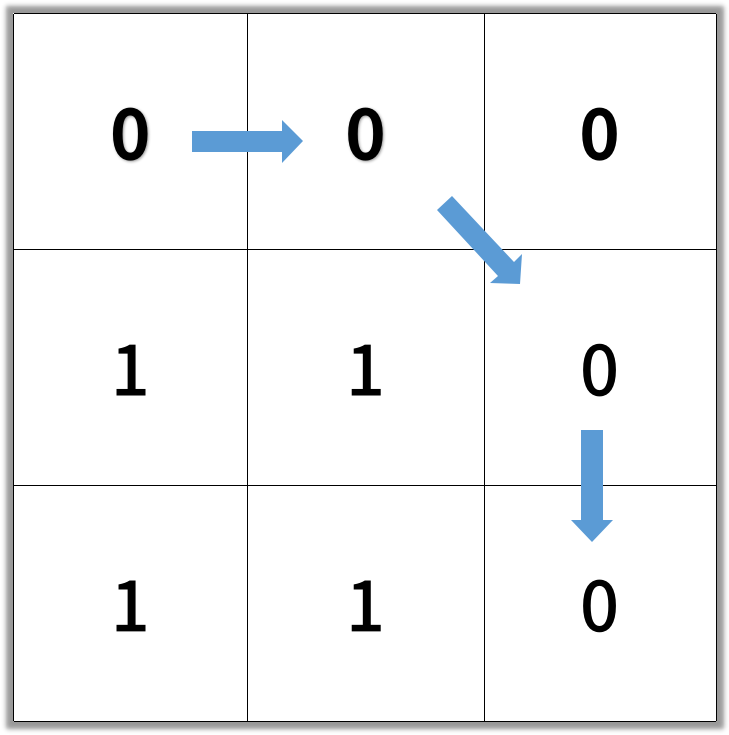
输入:[[0,0,0],[1,1,0],[1,1,0]]
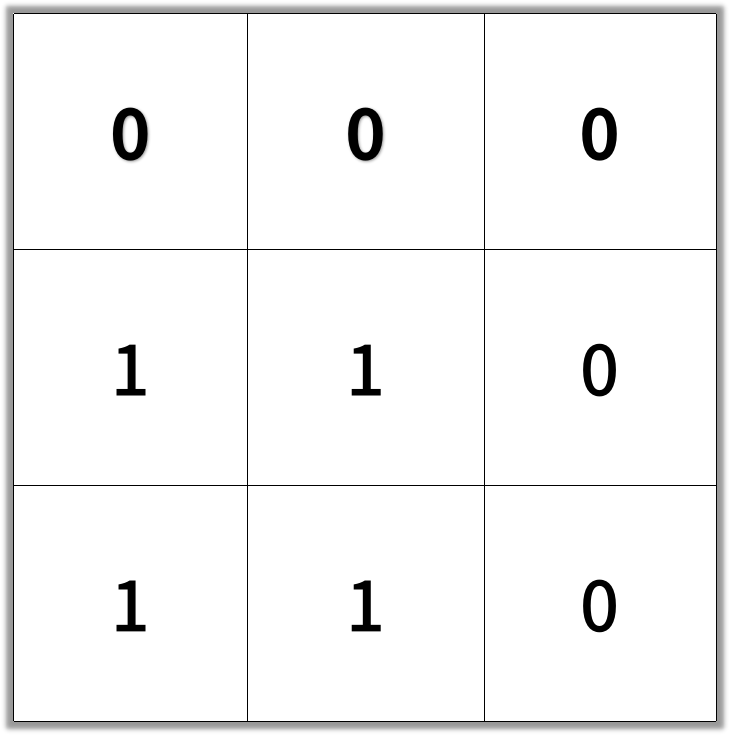 输出:4
输出:4
提示:
1 <= grid.length == grid[0].length <= 100 grid[i][j] 为 0 或 1
解法一
bfs
class Solution:
def shortestPathBinaryMatrix(self, grid: List[List[int]]) -> int:
q, n = [(0, 0, 2)], len(grid) # (起点, 终点, 步数)
if grid[0][0] or grid[-1][-1]: # 如果左上角(起点)和右下角(终点) 有一个为 1, 则永远都走不出去
return -1
elif n <= 2:
return n
for i, j, d in q:
for x, y in [(i-1, j-1), (i-1, j), (i-1, j+1), (i, j-1), (i, j+1), (i+1, j-1), (i+1, j), (i+1, j+1)]:
if 0 <= x < n and 0 <= y < n and not grid[x][y]:
if x == n - 1 and y == n - 1:
return d
q += [(x, y, d + 1)]
grid[x][y] = 1
return -1
解法二
A*
估价函数: h(current_point) = dist(current_point, destination_point)
https://dataaspirant.com/2015/04/11/five-most-popular-similarity-measures-implementation-in-python/
https://leetcode.com/problems/shortest-path-in-binary-matrix/discuss/313347/A*-search-in-Python/